36. Valid Sudoku

数独问题和八皇后问题，都是回溯法（backtracking）的经典案例，就像LIS/LCS问题是DP的经典案例一样。

回溯法通俗点说就是不断试错，如果某一步走错了，就退回上一步重新选择。关键是要抽象出一个“状态”的概念，而且这个状态必须是可以rollback的。计算过程有点类似数学中“全排列”的概念。而且一般会用到递归。

数独的玩法很简单，用1~9填充所有的空格，规则只有3条：

• 每一行不能有重复的数字
• 每一列不能有重复的数字
• 每一个小九宫格中，不能有重复的数字。比如下方的数独，有9个小九宫格，我们假设他们的编号是0-8。

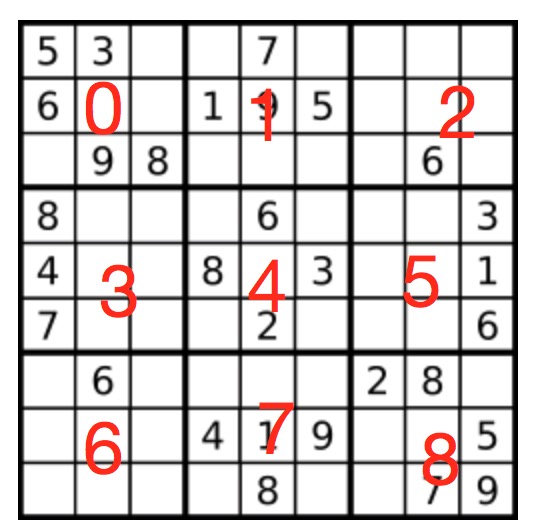
我们先抛开这道题目，写一个通用的数独生成程序。对于理解数独和回溯法都有很大好处。

public class Solution {
    // 生成所有可能的9x9数独
    public void genSudoku() {
        // 这3个二维数组用于保存当前的状态
        // 如果rowFlag[i][j]==1，说明第i行已经有数字j出现过了，不能再选
        // 同样如果colFlag[i][j]==1，说明第i列已经有数字j出现过
        // cubeFlag[i][j]==1说明第i个小九宫格中已经有数字j出现过
        // 我为了方便将数组的size设为10，因为每个格子可能填写的数字是1-9，可以直接写rowFlag[3][9]=1之类的，要不还要手动处理数组边界问题
        int[][] rowFlag = new int[10][10];
        int[][] colFlag = new int[10][10];
        int[][] cubeFlag = new int[10][10];
        // 这个char[][]用于存储最终的结果
        char[][] board = new char[9][9];
        // 从[0,0]这个格子开始填写数字
        fillBoard(board, 0, 0, rowFlag, colFlag, cubeFlag);
    }

    public void fillBoard(char[][] board, int row, int col, int[][] rowFlag, int[][] colFlag, int[][] cubeFlag) {
        // 先计算出[row,col]这个元素，属于第几个小九宫格
        int cubeNum = (row / 3) * 3 + col / 3;
        // 这个格子可能填写1~9，一个个试过去
        for (int i = 1; i <= 9; i++) {
            // 判断当前格子是否可以填写数字i
            if (rowFlag[row][i] == 0 && colFlag[col][i] == 0 && cubeFlag[cubeNum][i] == 0) {
                // 如果可以填写数字i，就更新状态，并且继续尝试下一个格子
                board[row][col] = (char) ('0' + i);
                rowFlag[row][i] = 1;  // 注意这里的状态变化
                colFlag[col][i] = 1;
                cubeFlag[cubeNum][i] = 1;
                //System.out.println("choose " + i + " for cell (" + row + "," + col + ")");
                // 找出要填写的下一个格子，注意这里的判断条件
                // 我的填写顺序是从左向右，从上到下
                if (col < 8)
                    fillBoard(board, row, col + 1, rowFlag, colFlag, cubeFlag);
                else if (row < 8)
                    fillBoard(board, row + 1, 0, rowFlag, colFlag, cubeFlag);
                else
                    printBorad(board);   // 已经没有格子需要填了，当前格子是最后一个格子，说明当前board已经存储了一个正确的解法，打印出来

                // 别忘了状态的rollback，先把状态恢复过来，才能尝试下一个数字
                // 每次尝试时，状态必须是相同的
                rowFlag[row][i] = 0;
                colFlag[col][i] = 0;
                cubeFlag[cubeNum][i] = 0;
            }
        }
    }
    // debug用，输出一个数独
    public void printBorad(char[][] board) {
        for (int i = 0; i < 9; i++) {
            System.out.println(Arrays.toString(board[i]));
        }
        System.out.println(" ");
    }
}

理论上这段程序可以计算出所有可能的9x9数独，但我没想到解法居然有这么多。。。大概是10^21的级别，参考这篇文章和Wiki。不过不要在意这些细节。。。关键是理解计算原理。

知道了原理，这道题目就非常简单了。这道题目只要求填入的数字满足那3条要求，甚至不要求有正确的解。对上面的数独生成程序稍微改改就可以了：

public class Solution {
    public boolean isValidSudoku(char[][] board) {
        // 其实一般人会用Map去存储状态吧，但我不知为何第一反应就是数组。。。
        int[][] rowFlag = new int[10][10];
        int[][] colFlag = new int[10][10];
        int[][] cubeFlag = new int[10][10];

        // 遍历给定的数独
        for (int row = 0; row < 9; row++) {
            for (int col = 0; col < 9; col++) {
                if (board[row][col] == '.')
                    continue;
                int cubeNum = (row / 3) * 3 + col / 3;
                // 当前格子填的数字是啥？
                // 注意下这种从char变int的方法
                int value = board[row][col] - '0';

                // 检查当前格子中的数字是否符合条件
                if (rowFlag[row][value] == 1 || colFlag[col][value] == 1 || cubeFlag[cubeNum][value] == 1)
                    return false;
                // 更新状态
                rowFlag[row][value] = 1;
                colFlag[col][value] = 1;
                cubeFlag[cubeNum][value] = 1;
            }
        }

        return true;
    }
}