5. Longest Palindromic Substring

求一个字符串中的最长回文字符串。

这道题卡了我很长时间。。。看到这道题目，第一反应就是dp。结果证明我的直觉很正确，确实可以用dp来解，但我却找错了状态方程。。。

当时我的定义是：dp(i)表示以char[i]字符结尾的最长回文字符串的长度。于是dp(0)、dp(1)都很好求出，但如何从dp(i)推导出dp(i+1)？当时我只考虑到一种情况：if(char[i+1]==char[i-dp(i)]) then dp(i+1)=dp(i)+2，但不止这一种情况啊。。。其他情况下dp(i+1)的值不仅仅依赖于以前的状态，想求出dp(i+1)就要遍历以前的字符，这就违反了dp的基本原则。沿着这个思路走下去，于是纠结了很长时间。。。

正确的做法是用二维dp：dp(i,j)==1表示从char[i]到char[j]是回文，否则dp(i,j)==0。我们可以认为这是一个i*j的矩阵，要算出这个矩阵中所有的元素的值。目的就是找到一个dp(i,j)==1的元素，使j-i+1最大。

状态转移方程：

if(dp[i][j]==0)
    dp[i-1][j+1]=0;
else if(char[i-1]==char[j+1])
    dp[i-1][j+1]=1;
else
    dp[i-1][j+1]=0;

画个图可能好理解些：在这个i*j的矩阵中，所有的dp(i,i)都必定是1，因为单独的一个字符都被认为是回文；所有的dp(i,i+1)也可以很简单的求出，因为只有2个字符，如果这两个字符相同，那么dp(i,i+1)=1，否则dp(i,i+1)=0。这个就是初始状态。

接下来就要根据初始状态和状态转移方程，求出矩阵中其他元素的值。由状态转移方程可知每个元素的值只跟它左下方的相邻元素有关。所以我们可以从已知的元素出发，向右上角“移动”，求出所有元素的值。矩阵的下半部份是不用关心的，因为i<j没有意义。

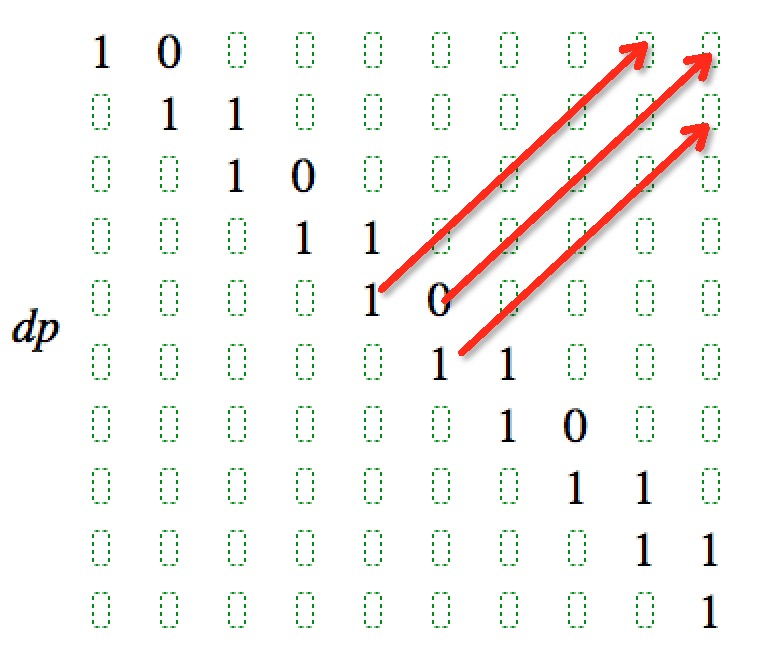
在实际计算过程中，没必要求出所有元素，否则容易TLE。如果当前元素是0，那么也不用往右上角“移动”了，肯定都是0。

public class Solution {
    // dp矩阵
    int[][] cache = null;

    public String longestPalindrome(String s) {
        if (s == null || s.trim().length() == 0)
            return null;

        char[] array = s.toCharArray();
        cache = new int[array.length][array.length];

        // 存储最长回文字符串的开始下标和长度
        int begin = 0, length = 0;
        // 遍历一次，计算初始状态，就是计算所有的dp(i,i)和dp(i,i+1)
        for (int i = 0; i < array.length; i++) {
            cache[i][i] = 1;
            if (i + 1 < array.length && array[i] == array[i + 1]) {
                cache[i][i + 1] = 1;
                begin = i;
                length = 2;
            }
        }

        if (length == 0) {
            begin = 0;
            length = 1;
        }

        // 开始计算矩阵中其他元素的值
        for (int i = 0; i < array.length; i++) {
            // 先尝试从dp(i,i)向右上角移动
            int trueStep = trueStep(array, i, i);  // 最多可以向右上角移动多少步？
            int trueDist = trueStep * 2 + 1;  // 这里利用了一个特性，每向右上角移动一步，长度+2
            if (trueDist > length) {
                begin = i - trueStep;
                length = trueDist;
            }

            // 再尝试从dp(i,i+1)向右上角移动
            if (i + 1 < array.length) {
                trueStep = trueStep(array, i, i + 1);
                trueDist = trueStep * 2 + 2;
                if (trueDist > length) {
                    begin = i - trueStep;
                    length = trueDist;
                }
            }
        }

        return s.substring(begin, length + begin);
    }

    /**从dp(row,col)开始，最多可以向右上角移动几步，碰到0或者越界就返回*/
    private int trueStep(char[] array, int row, int col) {
        // 如果当前元素是0，直接返回
        if (cache[row][col] != 1) {
            return 0;
        }
        int step = 0;
        while (row >= 0 && col < array.length) {
            if (array[row] == array[col]) {
                // dp(row,col)=1，说明从row到col是回文
                step++;
            } else {
                // 如果一个元素是0，那么接下来的也必然都是0，不用再算了
                break;
            }
            row--;
            col++;
        }
        return step - 1;
    }
}

其实还是有些可以优化的地方的，比如从某个元素向右上角移动时，可以算出最大可能移动多少步，如果最大可能步数都小于当前的trueStep，这一条线上的元素都不用计算了。

被dp折磨之后，我又google了下其他解法。其实这道题不一定要dp的，比如下面这个：

public class Solution {
    public String longestPalindrome(String s) {
        if (s == null) {
            return "";
        }
        char[] arr = s.toCharArray();
        int max = 0;
        int maxi = 0;
        int maxj = 0;

        for (int i = 0; i < arr.length;) {
            // 这里利用了回文字符串的特性：中间是一个或多个相同元素，然后加上对称的“两翼”，类似abcdxxxxxdcba
            // 一个中心两个基本点么。。。
            int i1 = getFarestSameElementIndex(arr, i);
            int dist = getDistance(arr, i, i1);   // 求出“两翼”的长度
            int index1 = i - dist;
            int index2 = i1 + dist;
            int l = index2 - index1;   // 这是中心包含arr[i]元素的，最大回文字符串的，长度
            if (l > max) {
                max = l;
                maxi = index1;
                maxj = index2;
            }
            i = i1 + 1;  // 这是最关键的一步，为何i=i1+1，而不是i++？
        }

        return s.substring(maxi, maxj + 1);
    }

    // 从index1/index2开始向左/右“扩展”，找到最大的回文字符串长度
    // 从arr[index1]到arr[index2]都是相同的元素
    private int getDistance(char[] arr, int index1, int index2) {
        int i1 = index1 - 1;
        int i2 = index2 + 1;
        int dist = 0;
        while (i1 >= 0 && i2 < arr.length) {
            if (arr[i1] == arr[i2]) {
                dist++;
            } else {
                break;
            }
            i1--;
            i2++;
        }
        return dist;
    }

    // 从index开始向右，找到最远的、相同元素的下标
    private int getFarestSameElementIndex(char[] arr, int index) {
        for (int i = index + 1; i < arr.length; i++) {
            if (arr[i] != arr[index]) {
                return i - 1;
            }
        }
        return arr.length - 1;
    }
}

这个解法比DP快很多。关键在于利用了回文字符串的特性，比较难想到。i = i1 + 1那步是关键，可以减少很多无用的计算量。